FP_ATAN2

좌표 데이터를 라디안으로 변환

이 FP 명령은 -p ~ +p 범위 내에서 데카르트 좌표(x,y)의 각도 j를 반환합니다.

파라미터

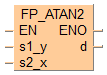
입력

s1_y (ANY_REAL): 데카르트 y 좌표
s2_x (ANY_REAL): 데카르트 x 좌표

출력

d (REAL): 결과(라디안)

주석

2차원 좌표의 각 위치 P는 데카르트 좌표 P(x,y) 또는 극좌표 P(r,j)(r = 반경, j = 각도)로 정의할 수 있습니다.

FP_ATAN2는 다음과 같이 정의합니다.

ATAN2_YX(y,x)	x	y
	x > 0
	x < 0	y ³ 0
	x < 0	y < 0
	x = 0	y > 0
		y < 0
연산 에러		y = 0

에러 플래그

sys_bIsOperationErrorHold(TRUE로 전환되어 TRUE로 유지됨)

인덱스 한정자를 사용하여 지정한 영역이 제한을 초과하는 경우.
s1_y(y 좌표) 또는 s2_x(x 좌표)에 실수가 아닌 수가 지정되는 경우
s1_y(y 좌표)에 0,0이 지정되고 s2_x(x 좌표)에 0,0이 지정되는 경우

예

POU 헤더

이 펑션 프로그램 시 사용한 모든 입력과 출력 변수는 POU 헤더에서 선언되었습니다. 모든 프로그래밍 언어에 같은 POU 헤더를 사용합니다.

	VAR
		bStart: BOOL:=FALSE;
			(*activates the instruction*)
		rPhi1Rad: REAL:=0.0;
		rPhi1Degree: REAL:=0.0;
	END_VAR
	VAR CONSTANT
		DEGR_OF_RAD: REAL:=57.295779513082320876798154814105;
	END_VAR
	VAR
	END_VAR

LD 본문

변수 bStart가 TRUE로 설정되면 펑션이 실행됩니다.

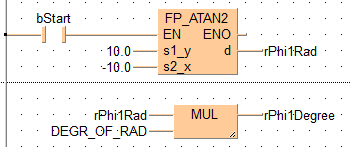
BODY
    WORKSPACE
        NETWORK_LIST_TYPE := NWTYPELD ;
        ACTIVE_NETWORK := 0 ;
    END_WORKSPACE
    NET_WORK
        NETWORK_TYPE := NWTYPELD ;
        NETWORK_LABEL :=  ;
        NETWORK_TITLE :=  ;
        NETWORK_HEIGHT := 6 ;
        NETWORK_BODY
B(B_F,FP_ATAN2!,,10,1,16,6,,?DEN?Ds1_y?Ds2_x?AENO?Cd);
B(B_VARIN,,10.0,8,3,10,5,);
B(B_VARIN,,-10.0,8,4,10,6,);
B(B_VAROUT,,rPhi1Rad,16,3,18,5,);
B(B_CONTACT,,bStart,3,2,5,4,);
L(1,3,3,3);
L(5,3,10,3);
L(1,0,1,6);
        END_NETWORK_BODY
    END_NET_WORK
    NET_WORK
        NETWORK_TYPE := NWTYPELD ;
        NETWORK_LABEL :=  ;
        NETWORK_TITLE :=  ;
        NETWORK_HEIGHT := 5 ;
        NETWORK_BODY
B(B_F,@MUL-2!,,11,1,16,4,,?D?D?C);
B(B_VARIN,,rPhi1Rad,9,1,11,3,);
B(B_VARIN,,DEGR_OF_RAD,9,2,11,4,);
B(B_VAROUT,,rPhi1Degree,16,1,18,3,);
L(1,0,1,5);
        END_NETWORK_BODY
    END_NET_WORK
END_BODY

ST 본문

rPhi1Rad:=ATAN2_YX(y := 10.0, x := -10.0); (* Result: 2.3561947 *)
rPhi1Degree := rPhi1Rad * DEGR_OF_RAD;     (* Result: 135.00002 *)