ATAN2_YX_LREAL

Returns the angle φ of the Cartesian coordinates (x,y) with LREAL arguments

ATAN2_YX_LREAL returns the angle j of the Cartesian coordinates (x,y) within the range of -p to +p.

Parameters

Input

y (LREAL): Cartesian y coordinate
x (LREAL): Cartesian x coordinate

Output

VAR_OUT (LREAL): result in radians

Remarks

Each position P of the two-dimensional coordinates can be defined by Cartesian coordinates P(x,y) or by polar coordinates P(r,j) (r = radius, j = angle).

Define ATAN2_YX as follows:

ATAN2_YX(y,x)	x	y
	x > 0
	x < 0	y ³ 0
	x < 0	y < 0
	x = 0	y > 0
		y < 0
0		y = 0

Example

POU header

All input and output variables used for programming this function have been declared in the POU header. The same POU header is used for all programming languages.

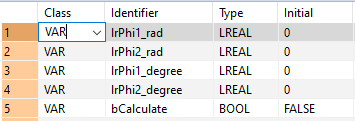
	VAR
		rPhi1Rad: REAL:=0.0;
		rPhi2Rad: REAL:=0.0;
		rPhi1Degree: REAL:=0.0;
		rPhi2Degree: REAL:=0.0;
	END_VAR	VAR CONSTANT 
		DEGR_OF_RAD: REAL:=57.295779513082320876798154814105;
	END_VAR
	VAR 
		bCalculatePhi1: BOOL:=FALSE;
	END_VAR

LD body

BODY
    WORKSPACE
        NETWORK_LIST_TYPE := NWTYPELD ;
    END_WORKSPACE
    NET_WORK
        NETWORK_TYPE := NWTYPELD ;
        NETWORK_LABEL :=  ;
        NETWORK_TITLE :=  ;
        NETWORK_HEIGHT := 3 ;
        NETWORK_BODY
B(B_COMMENT,,Calculate the angle values of point in quadrant 2,3,1,32,2,);
L(1,0,1,3);
        END_NETWORK_BODY
    END_NET_WORK
    NET_WORK
        NETWORK_TYPE := NWTYPELD ;
        NETWORK_LABEL :=  ;
        NETWORK_TITLE :=  ;
        NETWORK_HEIGHT := 5 ;
        NETWORK_BODY
B(B_COMMENT,,Result: 2.356194490192345,42,1,55,2,);
B(B_CONTACT,,bCalculate,9,1,11,3,);
B(B_F,E_ATAN2_YX_LREAL!,,26,0,36,5,,?DEN?Dy?Dx?AENO?C);
B(B_VARIN,,10,24,2,26,4,);
B(B_VAROUT,,lrPhi1_rad,36,2,38,4,);
B(B_VARIN,,-10,24,3,26,5,);
L(1,0,1,5);
L(1,2,9,2);
L(11,2,26,2);
        END_NETWORK_BODY
    END_NET_WORK
    NET_WORK
        NETWORK_TYPE := NWTYPELD ;
        NETWORK_LABEL :=  ;
        NETWORK_TITLE :=  ;
        NETWORK_HEIGHT := 4 ;
        NETWORK_BODY
B(B_COMMENT,,Result: 135.0,42,1,55,2,);
B(B_CONTACT,,bCalculate,9,1,11,3,);
B(B_F,FP_DEG!,,26,0,32,4,,?DEN?D@'s'?AENO?Cd);
B(B_VARIN,,lrPhi1_rad,24,2,26,4,);
B(B_VAROUT,,lrPhi1_degree,32,2,34,4,);
L(1,0,1,4);
L(1,2,9,2);
L(11,2,26,2);
        END_NETWORK_BODY
    END_NET_WORK
    NET_WORK
        NETWORK_TYPE := NWTYPELD ;
        NETWORK_LABEL :=  ;
        NETWORK_TITLE :=  ;
        NETWORK_HEIGHT := 3 ;
        NETWORK_BODY
B(B_COMMENT,,Calculate the angle values of point in quadrant 4,3,1,32,2,);
L(1,0,1,3);
        END_NETWORK_BODY
    END_NET_WORK
    NET_WORK
        NETWORK_TYPE := NWTYPELD ;
        NETWORK_LABEL :=  ;
        NETWORK_TITLE :=  ;
        NETWORK_HEIGHT := 5 ;
        NETWORK_BODY
B(B_COMMENT,,Result: -0.7853981633974483,42,1,55,2,);
B(B_CONTACT,,bCalculate,9,1,11,3,);
B(B_F,E_ATAN2_YX_LREAL!,,26,0,36,5,,?DEN?Dy?Dx?AENO?C);
B(B_VARIN,,-5,24,2,26,4,);
B(B_VAROUT,,lrPhi2_rad,36,2,38,4,);
B(B_VARIN,,5,24,3,26,5,);
L(1,0,1,5);
L(1,2,9,2);
L(11,2,26,2);
        END_NETWORK_BODY
    END_NET_WORK
    NET_WORK
        NETWORK_TYPE := NWTYPELD ;
        NETWORK_LABEL :=  ;
        NETWORK_TITLE :=  ;
        NETWORK_HEIGHT := 4 ;
        NETWORK_BODY
B(B_COMMENT,,Result: -45.0,42,1,55,2,);
B(B_CONTACT,,bCalculate,9,1,11,3,);
B(B_F,FP_DEG!,,26,0,32,4,,?DEN?D@'s'?AENO?Cd);
B(B_VARIN,,lrPhi2_rad,24,2,26,4,);
B(B_VAROUT,,lrPhi2_degree,32,2,34,4,);
L(1,0,1,4);
L(1,2,9,2);
L(11,2,26,2);
        END_NETWORK_BODY
    END_NET_WORK
END_BODY

ST body

//Calculate the angle values of point in quadrant 2
if (bCalculate) then
	lrPhi1_rad := ATAN2_YX_LREAL(y := 10.0, x := -10.0); 	// Result: 2.356194490192345
	FP_DEG(s := lrPhi1_rad, d => lrPhi1_degree);			// Result: 135.0
end_if;

//Angle value of point in quadrant 4
if (bCalculate) then
	lrPhi2_rad := ATAN2_YX_LREAL(y := -5.0, x := 5.0); 	// Result: -0.7853981633974483
	FP_DEG(s := lrPhi2_rad, d => lrPhi2_degree);		// Result: -45.0
end_if;